Breve rassegna delle principali alcune funzioni definite in EXCEL e OpenOffice-Calc per l'analisi statistica dei dati.
Il nome delle funzioni cambia a seconda della lingua con cui si è istallato Office (OpenOffice). L'elenco dei nomi delle funzioni con la traduzione in Italiano e Inglese si trova qui
Nota: per dividere gli argomenti delle funzioni EXCEL e Oo-Calc utilizzano, a seconda delle impostazioni, il punto e virgola (;) se il separatore dei decimali è una virgola (,) o la virgola (,) se il separatore dei decimali è un punto (.). Controllare le proprie inpostazioni!
|
Link utili
|
Sintesi numerica |
Tabelle di Frequenza |
|
Distribuzioni di Probabilità discrete Distribuzione binomiale Distribuzione di Poisson |
Distribuzioni di Probabilità continue Gauss (Normale) t-Student chi2 |
MEDIA(DATI) # Media di un insieme di dati MODA(DATI) # Moda di un insiem di dati MEDIANA(DATI) # Mediana di un insiem di dati
DEV.ST(DATI) # Deviaizone standard campionaria dei DATI VAR(DATI) # Varianza campionaria campionaria dei DATI QUARTILE(DATI,Q) # Valore del Quartile Q dei dati MAX(DATI)-MIN(DATI) # Range QUARTILE(DATI,3)-QUARTILE(DATI,1) # Distanza interquartileNote:
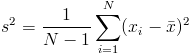
CURTOSI(DATI) # Indice di Curtosi dei dati ASIMMETRIA(DATI) # Indice di Skewness dei dati
CONTA.SE(DATI,CRITERI)Restituisce il numero di volte che un dato dell'insieme DATI soddisfa i CRITERI dati. Da non usare nel caso di dati ordinali.
FREQUENZA(DATI,X)Restituisce la frequenza assoluta integrata dei dati per il valore X, ovvero il numero di dati con valore inferiore o eguale a X. La frequenza relativa intagrata si ottine dividendo per il numero dei dati nella matrice dati. La frequenza assoluta di una data classe (Xa,Xb], ovvero il numero di dati tali che:
si ottiene come differenza:
DISTRIB.BINOM(N_successi,N_prove,P_successo,Cumulativo)dove:
=DISTRIB.BINOM(3,7,0.3,0)Calcola la probabilità di ottenere 3 successi su 7 prove quando la probabilità di successo sia 0.3
=DISTRIB.BINOM(5,7,0.3,1)Calcola la probabilità di ottenere fino a 5 successi su 7 prove quando la probabilità di successo sia 0.3
=1 - DISTRIB.BINOM(5,7,0.3,1)Calcola la probabilità di ottenere almeno 4 successi su 7 prove quando la probabilità di successo sia 0.3
=POISSON(m,Atteso,Cumulativo)m è il numero degli eventi per il quale calcolare la probabilità, deve essere un numero intero;
Esempi
= POISSON(4,6.5,0)Calcola la probabilità di ottenere 4 conteggi quando il valore atteso è x=6.5
= POISSON(4,6.5,1)Calcola la probabilità di ottenere al massimo 3 conteggi quando il valore atteso è x=6.5
= 1-POISSON(0,6.5,1)Calcola la probabilità di ottenere un numero di conteggi diverso da 0 quando il valore atteso è x=6.5
= POISSON(5,6.5,1) - POISSON(2,6.5,1)Calcola la probabilità di ottenere 3, 4 oppure 5 conteggi quando il valore atteso è x=6.5
, la sua inversa:
DISTRIB.NORM(x,Media,DevSt,Cumulativo)calcola la F(x) (se Cumulativo=1) o la p(x) (se Cumulativo=0) per una distribuzione di Gauss con valore aspettato m=Media e deviazione standard s =DevSt.
DISTRIB.NORM.ST(z)calcola la F(z) per una variabile aleatoria che segue una distribuzione normale standardizzata, ovvero con valore aspettato nullo: m=0 e deviazione standard unitaria: s =1.0.
Esempi
= DISTRIB.NORM(7.0,6.5,2.2,0)Calcola la densità di probabilità p(x) per una variabile aleatoria X che segue una distribuzione normale con valore atteso s=6.5 e deviazione standard s=2.2:
= DISTRIB.NORM(7.0,6.5,2.2,1)Calcola la probabilità di osservare un valore minore o uguale a 7.0 per una variabile aleatoria X che segue una distribuzione normale con valore atteso s=6.5 e deviazione standard s=2.2:
= DISTRIB.NORM(7.0,6.5,2.2,1) - DISTRIB.NORM(5.0,6.5,2.2,1)Calcola la probabilità di osservare un valore compreso tra 5.0 e 7.0 per una variabile aleatoria X che segue una distribuzione normale con valore atteso s=6.5 e deviazione standard s=2.2:
= 1-DISTRIB.NORM(7.0,6.5,2.2,1)Calcola la probabilità di osservare un valore maggiore di 7.0 per una variabile aleatoria X che segue una distribuzione normale con valore atteso s=6.5 e deviazione standard s=2.2:
= DISTRIB.NORM.ST(-1.96)Calcola la probabilità di osservare un valore minore di -1.96 per una variabile aleatoria X che segue una distribuzione normale standardizzata:
= 2*DISTRIB.NORM.ST(-1.96)Calcola la probabilità di osservare un valore minore di -1.96 oppure maggiore di 1.96 per una variabile aleatoria X che segue una distribuzione normale standardizzata.
= DISTRIB.NORM.ST(1.96) - DISTRIB.NORM.ST(-1.96)Calcola la probabilità di osservare un valore compreso nell'intervallo [-1.96,1.96] per una variabile aleatoria X che segue una distribuzione normale standardizzata.
La funzione EXCEL (Oo-Calc):
INV.NORM(p,Media,DevSt)calcola il valore di x per cui la F(x) = p dove F(x) è la distribuzione di Gauss.
INV.NORM.ST(p)calcola il valore di z per cui F(z) = p dove F(z) è la distribuzione di Gauss standardizzata. La funzione INV.NORM.ST(p) è l'analogo della funzione Gnuplot invnorm(x)
Esempi
= INV.NORM(0.025,6.5,2.2)Calcola il valore della variabile aleatoria X=x tale che la probabilità osservare un valore inferiore a x è proprio: P(X<x)=0.025 .
= 1-INV.NORM(0.975,6.5,2.2)Calcola il valore della variabile aleatoria X=x tale che la probabilità osservare un valore maggiore di a x è proprio: P(X>x)=0.975 .
il valor medio e s la deviazione standard campionaria per un campione di numerosità N con valore atteso m, allora
è la deviazione standard della distribuzione delle medie campionarie e la variabile:
DISTRIB.T(tlim,n-lib,code)dove n-lib è il numero di gradi di libertà, è definita per t>0.
INV.T(p,n-lib)calcola il valore tlim per il quale p è la probabilità di osservare un valore della variabile t fuori dell'intervallo [-tlim,tlim]:
TEST.T(Dati_A,Dati_B,code,tipo)calcola la significativit\'a di un test t-Student.